两直线垂直,“”值积为问题引入如图(1),在平面直角坐标系中,直线,为常数,且与直线,垂直,求探究1如图(2),当直线二、四探究2将探究1中的直线,进行平移,平移后直线,的“_________变化(填“发生”或“不发生”),不发生平分线,直线经过原点时,易知直线____,探究3当直线经过原点,且非第一、三象限的角平分线,直线时,如图(3),在直线上任取一点,过点作轴于点线上任取一点,过点作轴于点图(3)设点的坐标为,...
两点之间,线段最短(将军饮马模型以及变形)以题串模型例1一题多问在平面直角坐标系中,,,,点轴上一动点,连接,,(1)当的值最小时,在图(1)中作出点的位置,小值为_图(1)[答案]如图(1)所示.如图(1)(2)当的值最小时,在图(2)中作出点的位置,小值为_图(2)[答案]如图(2)所示.图(2)(3)当的值最大时,在图(3)中作出点的位置,的最大值为_图(3)[答案]如图(3)所示.图(3)(4)当的值最大时,在图(...
建立平面直角坐标系解决与特殊四边形相关的线段长问题1.在求某些特殊四边形中线段的长时,对于某些以正方形、矩形、含或角的平行四边形或菱形为背景,尤其是涉及中点的题目,若一时找不到解题突破口,可考虑建立适当的平面直角坐标系,利用数形结合思想将其转化为两点间的距离问题.2.建立平面直角坐标系解决与特殊四边形相关的线段长问题的一般步骤:(1)建立恰当的平面直角坐标系,使与待求线段的端点相关的点的坐标、直线的表...
根据直线上点的坐标求“k”值思维引导系列一点(非原点)的坐标,求背景点是直线上一点(非原点),直线与轴所夹锐角为.推理过程将代入,得.图示及__重要结论1.函数的值等于其图象上任意一点(非原点)的纵坐标与横坐标之比.2.当时,等于直线与轴所夹锐角的正切值;当时,等于直线与轴所夹锐角的正切值的相反数.续表线上两点的坐标,求背景点,是直线上两点,直线与轴所夹锐角为.推理过程将,分别代入,得,得所以图示及与的关...
反比例函数中的常见模型探究系列以题串模型例1如图,直线,均经过原点,直线交于点,,直线与双曲线交于点,(1)线段线段_(2)顺次连接点,,,①四边形平行四边形②若,则___时,四边形5模型总结类型1对称模型如图,过原点的直线与双曲线交于点,重要结论:①点,关于点.例2一题多问如图(1),双曲线与矩形,.图()图()图()图()图()(1)如图(2),过点作于点,过点作于点①___=②连接,,求证:证明:,,,.③,的...
反比例函数中的几何意义的相关计算微点1以单函数图象为背景图形的顶点在反比例函数的图象上①②③④___.(填“”“______________________________点,关于原点对________________________________点,_________________________________点,关于原_____________________________________续表强化训练(第1题)1.[2023山东烟台]如图,在直角坐标系中,与于点,为的直径,点在函数的图象上,为轴上一点,的面积为6,则为____.24...
对角互补模型探究系列模型总结基本模型图示常用辅助线结论—模型①_____.基本模型图示常用辅助线结论—模型特殊地,点在的平分线上:_②_____;2.③____;3.,,之间续表基本模型图示常用辅助线结论—⑤_____.特殊地,点在的平分线上:⑥_____;2续表基本模型图示常用辅助线结论—模型⑨_____.续表基本模型图示常用辅助线结论特殊地,点在的平分线上:_⑩_____;2.⑪____;3.,,之间的数量关系为续表强化训练1.如图,在四边形中,...
动态直线问题的求解方法类型1旋转型动态直线问题图(1)问题引入1对于直线(为常数),随着的变化,直线(选填“旋转”“平移”或“对称”).在图(1)中画三条的直线旋转[答案]图略.图(2)问题引入2对于直线(式可化为(______),随着值的变化,直线点______,并绕点______作______变换(选填“旋转”“平移”或“对称”).在图(2)中画三条值不同的直线旋转[答案]图略.图(3)问题引入3对于直线(表达式可化为(______),...
动点的运动路径问题类型1直线类运动路径问题(第1题)1.如图,在矩形中,,,点为的中点,点为上一动点,将绕点,得到线段,连接,若点在矩形(包括边界),则6(第2题)2.如图,,点为射线上一定点,点射线上一动点,且点以每秒2个单位长度的速度从点出发向右运动,设运动时间为秒.连接,以右侧作等边三角形.当时,点___.6(第3题)3.如图,点在线段,,.点为线段上一动点,在动点从点运动到点的过程中,线段的中点长为_(...
半角模型探究系列以题串模型例1一题多问如图(1),四边形是正方形,分别与直线、直线交于点,,射线分别与直线线交于点,图(1)图(2)图(3)图(4)图(5)(1)当点在线段①如图(2),请延长到点,使,并证明[答案]如图(1).图(1)证明:连接,,,,,,.又,,②如图(3),将绕点顺时针旋转,得到,并证明图(2)[答案]如图(2).证明:连接由题意得,.,,,,.又,.(2)当点在线段①如图(4),,,②如图(5),,,...
“一线三等角”模型探究系列模型说明“一线三等角”模型指的是三个等角的顶点在同一条直线上的模型,也称为型”相似模型,如图,特别地,当模型类别及相关结论型:三等角在直线同侧燕尾型:直线穿过一等角锐角直角钝角锐角直角钝角重要结论:1.①______;2.若,则②______,③重要结论:1.;2.若,则.续表强化训练(第1题)1.[2023山东东营]如图,为等边三角形,点,分别在边,上,.若,则的CA.1.8B.2.4C.3D.3.2(第2题)2.如图,...
“手拉手”全等模型以题串模型例一题多问如图(1),在等腰三角形中,,点,分别为,上的点,且.将绕点接,.图(1)图(2)图(3)图(4)(1)图(1)中,与(2)在图(2)的情形下,求证:证明:,.又,,.(3)图(2)中,延长交于点,求的度数.(用含表示)[答案]设,交于点.,.又,.(4)当①与的②延长,交于点,则(5)当①与的②设,交于点,则模型总结如图,,,,将点旋转,直线,交于点,所夹较小的角为重要结论:1.点...
2024河北中考数学二轮复习专题四三角形、四边形实践探究专项训练类型一旋转问题典例精讲例(一题多设问)如图,C,D,E三点在线段AB上,且AC=CE=ED=DB,将线段AC绕点C按顺时针方向旋转α(0°<α<180°),点A的对应点为点A1.同时将线段DB绕点D按逆时针方向旋转β(0°<β<360°),点B的对应点为点B1.(1)如图①,若β=α,连接A1D,B1C,交于点F;①求证:△A1CD≌△B1DC;②求证:△FCD为等腰三角形;【思维教练】①由SAS证明...
2024河北中考数学二轮复习专题四三角形、四边形实践探究专项训练类型一旋转问题典例精讲例(一题多设问)如图,C,D,E三点在线段AB上,且AC=CE=ED=DB,将线段AC绕点C按顺时针方向旋转α(0°<α<180°),点A的对应点为点A1.同时将线段DB绕点D按逆时针方向旋转β(0°<β<360°),点B的对应点为点B1.(1)如图①,若β=α,连接A1D,B1C,交于点F;①求证:△A1CD≌△B1DC;②求证:△FCD为等腰三角形;【思维教练】①由SAS证明...
微专题遇到中点如何添加辅助线方法一构造中位线情形1图形中出现两个及以上的中点时,考虑连接两个中点构造中位线如图,已知点D、E分别为AB、AC的中点.【结论】DE∥BC,DE=12BC,△ADE∽△ABC.情形2图形中出现中点时,考虑过中点作另一边的平行线构造中位线如图,已知点D为AB的中点.【结论】AE=CE,DE=12BC,△ADE∽△ABC.1.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=6,则BF的长为()A...
微专题七大常考全等模型模型一平移型模型展示模型特点沿同一直线(BC)平移可得两三角形重合(BE=CF)解题思路证明三角形全等的关键:(1)加(减)共线部分CE,得BC=EF;(2)利用平行线性质找对应角相等1.如图,点C是AE的中点,∠A=∠ECD,AB=CD,若∠B=50°,则∠D的度数为()A.30°B.40°C.50°D.60°第1题图C2.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.第2题图证明: BE=CF,∴BE+EC=C...
微专题对称性质在折叠问题中的应用1.折叠问题常见的类型有:2.折叠问题的本质是全等变换,折叠前的部分与折叠后的部分是全等图形.①线段相等:ED′=______,EG=______,FD′=______;②角度相等:∠D′=________,∠D′EG=________;③全等关系:四边形FD′EG≌_____________.ADAGFD∠D∠DAG四边形FDAG3.折痕可看作垂直平分线:GF⊥________(折痕垂直平分连接两个对应点的连线).4.折痕可看作角平分线:∠EGF=______...
四种方法求阴影部分面积方法一直接公式法方法解读当阴影部分为扇形、三角形或特殊四边形时,直接用面积公式进行求解.方法示例1.(2023贺州)如图,在边长为2的等边△ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB,AC分别交于E,F两点,则图中阴影部分的面积为()A.B.C.D.第1题图方法应用63223C方法二和差法一、直接和差法方法示例阴影部分面积可以看成扇形、三角形、特殊四边形面积相加减.第2题图方法应用2.(...
2024贵州中考数学二轮复习专题题型五规律探索题专项训练类型一数式规律(黔西南州3考,黔东南州2考)考向1数字累加型基础小练(1)若一列正整数:1,2,3,4,5,,依照此规律,则第n(n≥1)个数是________,这n(n≥1)个数的和为________;(2)若一列数:1,3,5,7,9,,依照此规律,则第n(n≥1)个数是________,这n(n≥1)个数的和为________;(3)若一列数:2,4,6,8,10,,依照此规律,则第n(n≥1)个数是________,这n(n≥1)个...
2024贵州中考数学二轮复习专题题型五规律探索题专项训练类型一数式规律(黔西南州3考,黔东南州2考)考向1数字累加型基础小练(1)若一列正整数:1,2,3,4,5,,依照此规律,则第n(n≥1)个数是________,这n(n≥1)个数的和为________;(2)若一列数:1,3,5,7,9,,依照此规律,则第n(n≥1)个数是________,这n(n≥1)个数的和为________;(3)若一列数:2,4,6,8,10,,依照此规律,则第n(n≥1)个数是________,这n(n≥1)个...
 “马上有钱花”马年新年春节元旦暴富发财市集市游园会活动策划方案.pptx
8
60页
“马上有钱花”马年新年春节元旦暴富发财市集市游园会活动策划方案.pptx
8
60页
 HG-T 21581-2012.pdf
240
1190页
HG-T 21581-2012.pdf
240
1190页
 汉语拼音12ɑn en in un ün教学反思3.docx
150
1页
汉语拼音12ɑn en in un ün教学反思3.docx
150
1页
 三年级语文上册 期末全真模拟卷(重点小学)
81
7页
三年级语文上册 期末全真模拟卷(重点小学)
81
7页
 GB 55031-2022 民用建筑通用规范.pdf(24页)
1876
24页
GB 55031-2022 民用建筑通用规范.pdf(24页)
1876
24页
 19DX101-1建筑电气常用数据(带书签).pdf
3542
354页
19DX101-1建筑电气常用数据(带书签).pdf
3542
354页
 013130746-周岩彬-我国中小企业融资现状分析及对策研究
26
22页
013130746-周岩彬-我国中小企业融资现状分析及对策研究
26
22页
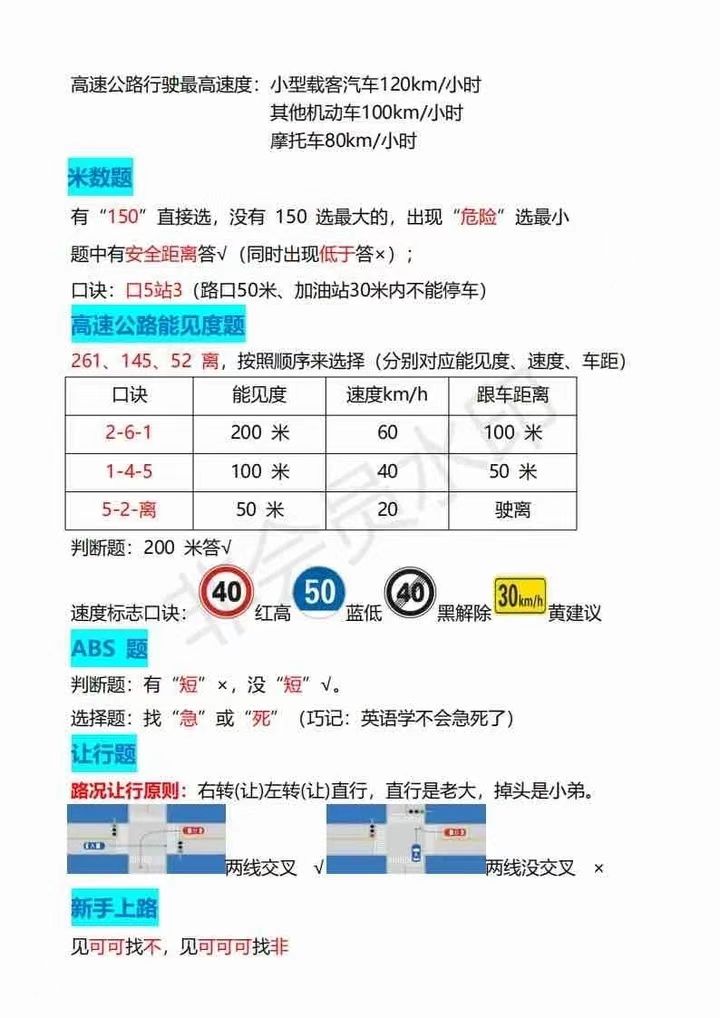 c48e30e2-c9bc-4b72-b502-9ebd011aff66.jpg
94
1页
c48e30e2-c9bc-4b72-b502-9ebd011aff66.jpg
94
1页
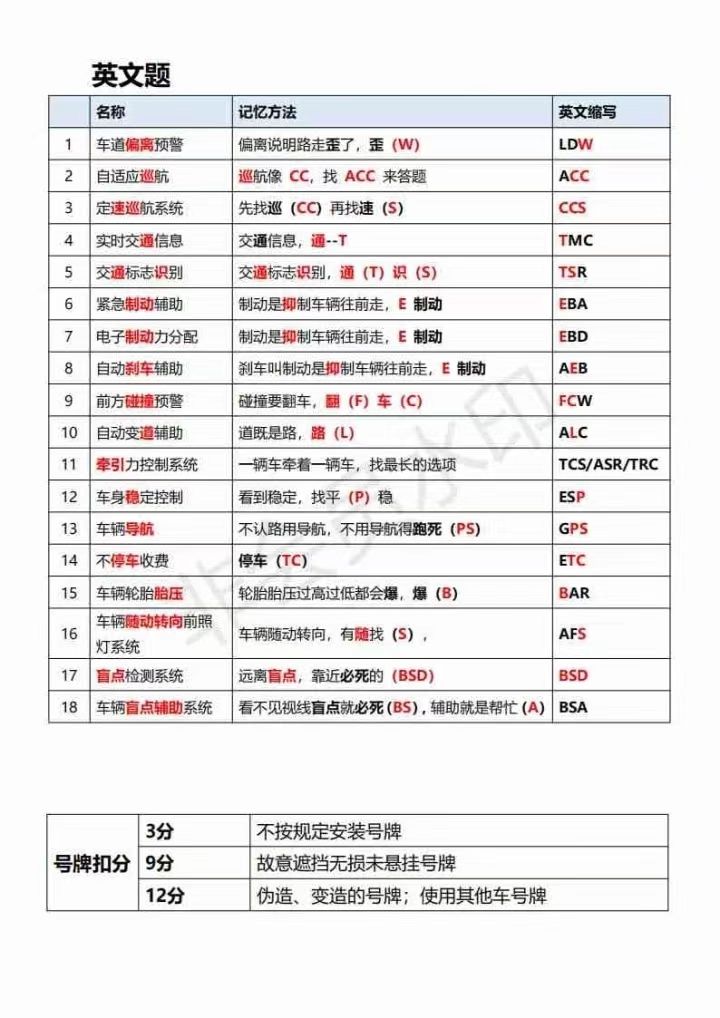 ecf20c37-28ed-40c5-83ba-0807cbebbbda.jpg
67
1页
ecf20c37-28ed-40c5-83ba-0807cbebbbda.jpg
67
1页
 牛魔网爱吃鱼
80
1页
牛魔网爱吃鱼
80
1页
 19DX101-1建筑电气常用数据(带书签).pdf
3542
354页
19DX101-1建筑电气常用数据(带书签).pdf
3542
354页
 GB 55031-2022 民用建筑通用规范.pdf(24页)
1876
24页
GB 55031-2022 民用建筑通用规范.pdf(24页)
1876
24页
 “马上有钱花”马年新年春节元旦暴富发财市集市游园会活动策划方案.pptx
8
60页
“马上有钱花”马年新年春节元旦暴富发财市集市游园会活动策划方案.pptx
8
60页
 竞争分析案例-豆瓣网1231
206
3页
竞争分析案例-豆瓣网1231
206
3页
 013130830-张赵红-企业存货管理存在的问题及对策—以长城经贸公司为例
88
13页
013130830-张赵红-企业存货管理存在的问题及对策—以长城经贸公司为例
88
13页
 HG-T 21581-2012.pdf
240
1190页
HG-T 21581-2012.pdf
240
1190页
 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》
17
27页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》
17
27页
 汉语拼音12ɑn en in un ün教学反思3.docx
150
1页
汉语拼音12ɑn en in un ün教学反思3.docx
150
1页
 2024年中考化学二轮题型突破限时精练 物质的检验、鉴别、除杂、共存(含解析).docx
45
37页
2024年中考化学二轮题型突破限时精练 物质的检验、鉴别、除杂、共存(含解析).docx
45
37页
 25年WP过AI率汉语言文学-论刘醒龙小说《天行者》中乡村教师“乐天苦行”的君子品格8.160.docx
30
19页
25年WP过AI率汉语言文学-论刘醒龙小说《天行者》中乡村教师“乐天苦行”的君子品格8.160.docx
30
19页

