2024陕西中考数学二轮专题训练题型二小几何压轴题类型一与线段有关的问题1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8.若点E、F是BC边上的两个动点,以EF为边的等边△EFP的顶点P在△ABC内部或边上,则等边△EFP的周长的最大值为________.第1题图2.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点D、E分别在AB、BC上,且以DE为直径的圆与AC相切,则DE的最小值为________.第2题图3.如图,在菱形ABCD中,AB=AC=10,对...
2024陕西中考数学二轮专题训练题型二小几何压轴题类型一与线段有关的问题1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8.若点E、F是BC边上的两个动点,以EF为边的等边△EFP的顶点P在△ABC内部或边上,则等边△EFP的周长的最大值为________.第1题图2.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点D、E分别在AB、BC上,且以DE为直径的圆与AC相切,则DE的最小值为________.第2题图3.如图,在菱形ABCD中,AB=AC=10,对...
2024陕西中考数学二轮专题训练题型八几何测量问题类型一与锐角三角函数有关的几何测量【类型解答】与锐角三角函数有关的几何测量应用题近10年解答题中考查3次,分值为6分或7分.考查特点:设问均为底部不可及的测量问题,且都是通过在两个直角三角形中解决问题.1.西安奥体中心体育馆是第十四届全运会的主场馆之一,其顶部有16个角舒展绽放,像盛开的花瓣.某日,家住附近的小华和小明想测量其中一个角顶部距离地面的高度AB,由...
2024陕西中考数学二轮专题训练题型八几何测量问题类型一与锐角三角函数有关的几何测量【类型解答】与锐角三角函数有关的几何测量应用题近10年解答题中考查3次,分值为6分或7分.考查特点:设问均为底部不可及的测量问题,且都是通过在两个直角三角形中解决问题.1.西安奥体中心体育馆是第十四届全运会的主场馆之一,其顶部有16个角舒展绽放,像盛开的花瓣.某日,家住附近的小华和小明想测量其中一个角顶部距离地面的高度AB,由...
2024陕西中考数学二轮专题训练方程、不等式的实际应用考向一购买、销售问题构建“总价=单价×数量”关系1.[数学文化]《九章算术》中方程篇记述这样一道题,原文如下:“今有牛五、羊二,直金十两.牛二、羊五,直金八两.问牛羊各直金几何?”大意为:今有牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两.问牛、羊每头各值金多少?请解答上述问题.2.某超市购进了一批袋装的米脂小米,平均每天可销售40袋,每袋盈利15元,...
学科网(北京)股份有限公司模型一“A”字模型图条件EF∥BC∠AED=∠B结论△AEF∽△ABC△ADE∽△ACB1.(2022巴中)如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC∶OC=1∶2,过点C作CD∥OB交AB于点D,C,D两点纵坐标分别为1,3,则B点的纵坐标为()第1题图A.4B.5C.6D.72.(2022东营)如图,在△ABC中,点F,G在边BC上,点E,H分别在边AB,AC上,四边形EFGH是矩形,EH=2EF,AD是△ABC的高,BC=8,AD=6,那么EH的长为....
二次函数与几何综合题类型一线段问题满分技法微技能一阶例1如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点P是抛物线第一象限内一动点,过点P作PH⊥x轴于点H,交直线BC于点Q.例1题图(2)设点P的横坐标为t,则点P的坐标可表示为________________,点Q的坐标可表示为____________,点H的坐标可表示为________;(t,-t2+2t+3)(t,-t+3)(t,0)(1)点A的坐标为__________,点B的坐标为___________,点C的坐标为__...
二次函数与几何综合题类型五与角度有关的问题微技能一阶例1如图,在平面直角坐标系中,点B的坐标为(1,0),点A在第一象限,且AB⊥x轴于点B,若∠AOB=30°,则点A的坐标为___________.例1题图(1,)33例2如图,在平面直角坐标系中,点A的坐标为(-1,0),点B的坐标为(2,0),点P为直线y=1上一点,若∠APB=90°,则点P的坐标为________________________________.例2题图(,1)或(,1)152152例3如图,在平面直角坐标系中,已...
二次函数与几何综合题类型四特殊四边形存在性问题微技能一阶例1如图,已知平面上不共线的三个点A、B、C,请在平面内找一点P,使以A、B、C、P为顶点的四边形是平行四边形,请在图中画出所有符合要求的点P.(保留作图痕迹,不写作法)例1题图P2P1P3例2在如图所示9×9的网格中,点A、B在格点上,请找出两组格点C、D,使得以A、B、C、D为顶点的四边形为平行四边形.例2题图解:分为两类:①以AB为边的平行四边形ABCD,举例如解图(答案...
二次函数与几何综合题类型三特殊三角形存在性问题微技能一阶例1如图,已知线段AB和直线l,请在直线l上找一点M,使△ABM是等腰三角形,请在图中画出所有符合要求的点M.(保留作图痕迹,不写作法)例1题图解:画图如解图所示.例1题解图例2如图,已知点A(-3,0),B(4,0),C(0,4),点P是线段BC上一动点,当以A、C、P为顶点的三角形是等腰三角形时,求点P的坐标.例2题图解:设直线BC的解析式为y=kx+b,将B(4,0),C(0,4)代入,...
二次函数与几何综合题类型二面积问题微技能一阶例1在平面直角坐标系中,抛物线y=-x2-2x+3的顶点为A,与y轴交于点B,与x轴交于C、D两点(点C在点D左侧).(1)如图①,过点A作AE⊥x轴于点E,求△ABE的面积;例1题图①解:(1)抛物线y=-x2-2x+3=-(x+1)2+4.∴点A的坐标为(-1,4),∴S△ABE=×1×4=2;12一题多设问满分技法直接公式法:适用于三角形的一边平行于坐标轴(或在坐标轴上),直接运用三角形的面积公式S=ABh求...
第35课时概率内蒙古中考真题及拓展21考点精讲概率的计算公式法列表法或画树状图法用频率估计概率几何概型游戏的公平性事件的分类必然事件不可能事件随机事件概率考点精讲【对接教材】北师:七下第六章P135~P159;九上第三章P59~P74;人教:九上第二十五章P126~P153.事件的分类1考点事件类型定义概率必然事件在一定条件下,必然会发生的事件________不可能事件在一定条件下,必然不会发生的事件________随机事件在一定条件下...
2024辽宁中考数学二轮专题训练微专题构造全等的四大方法方法一倍长中线法方法解读(1)倍长中线在△ABC中,AD是BC边的中线.辅助线作法:延长AD至点E,使AD=DE,连接BE.结论:△ACD≌①________.(2)倍长类中线在△ABC中,点D是边BC的中点,点E是边AB上一点,连接DE.辅助线作法:延长ED至点F,使DF=DE,连接CF.结论:△BDE≌②________.1.如图.AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点,连接AM.求证:DE=2AM.第1题图...
2024辽宁中考数学二轮专题训练微专题构造全等的四大方法方法一倍长中线法方法解读(1)倍长中线在△ABC中,AD是BC边的中线.辅助线作法:延长AD至点E,使AD=DE,连接BE.结论:△ACD≌①________.(2)倍长类中线在△ABC中,点D是边BC的中点,点E是边AB上一点,连接DE.辅助线作法:延长ED至点F,使DF=DE,连接CF.结论:△BDE≌②________.1.如图.AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点,连接AM.求证:DE=2AM.第1题图...
2024辽宁中考数学二轮专题训练构造2、3倍线段问题类型一利用等腰直角三角形构造含2倍关系的线段问题如图,在Rt△ABC中,∠BAC=90°,∠B=45°,过点A作AD⊥BC于点D.结论:BC=2AC=2AB;AB=AC=2AD=2BD=2DC.看到线段间含2倍关系或已知条件含45°角,等腰直角三角形判断线段数量关系时,考虑运用等腰直角三角形性质进行求解.练习1已知边长为4的正方形ABCD与边长为a(1<a<4)的正方形CFEG的顶点C重合.(1)如图①,若点E在对...
2024辽宁中考数学二轮专题训练构造、倍线段问题类型一利用等腰直角三角形构造含倍关系的线段问题如图,在Rt△ABC中,∠BAC=90°,∠B=45°,过点A作AD⊥BC于点D.结论:BC=AC=AB;AB=AC=AD=BD=DC.看到线段间含倍关系或已知条件含45°角,等腰直角三角形判断线段数量关系时,考虑运用等腰直角三角形性质进行求解.练习1已知边长为4的正方形ABCD与边长为a(1<a<4)的正方形CFEG的顶点C重合.(1)如图①,若点E在对角线AC上...
2024辽宁中考数学二轮专题训练题型一分析判断函数图象题类型一判断函数图象考向一面积与线段之间的关系典例精讲例1如图,在正方形ABCD中,AB=3,点E是边AB上一点(点E与点B不重合),点F是射线BC上一点,且∠EFB=30°,设BE=x,△BEF与正方形ABCD重叠部分的面积为S,则S关于x的函数图象大致为()例1题图【分层分析】第一段:当点F在线段BC上,此时,△BEF与正方形ABCD重叠部分即为________的面积, BE=x,∠EFB=30°,∴BF=...
2024辽宁中考数学二轮专题训练题型一分析判断函数图象题类型一判断函数图象考向一面积与线段之间的关系典例精讲例1如图,在正方形ABCD中,AB=3,点E是边AB上一点(点E与点B不重合),点F是射线BC上一点,且∠EFB=30°,设BE=x,△BEF与正方形ABCD重叠部分的面积为S,则S关于x的函数图象大致为()例1题图【分层分析】第一段:当点F在线段BC上,此时,△BEF与正方形ABCD重叠部分即为________的面积, BE=x,∠EFB=30°,∴BF=...
2024辽宁中考数学二轮专题训练题型五函数实际应用题(最值问题)突破设问一求函数关系式情形1题干中已知函数关系式典例精讲例1某商家销售一种农产品,若该农产品的种植成本为10元/斤,售价不低于15元/斤,每日销售量y(斤)与售价x(元/斤)之间满足如图所示的一次函数关系式,求y与x之间的函数关系式.【思维教练】欲求y与x之间的函数关系式,由题目可知,y与x之间满足一次函数关系式,则可设函数关系式为y=kx+b,由图象可知,一次...
2024辽宁中考数学二轮专题训练题型五函数实际应用题(最值问题)突破设问一求函数关系式情形1题干中已知函数关系式典例精讲例1某商家销售一种农产品,若该农产品的种植成本为10元/斤,售价不低于15元/斤,每日销售量y(斤)与售价x(元/斤)之间满足如图所示的一次函数关系式,求y与x之间的函数关系式.【思维教练】欲求y与x之间的函数关系式,由题目可知,y与x之间满足一次函数关系式,则可设函数关系式为y=kx+b,由图象可知,一次...
 2024年云南省中考数学试卷(含详细解析).pdf74315页
2024年云南省中考数学试卷(含详细解析).pdf74315页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip457
2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip457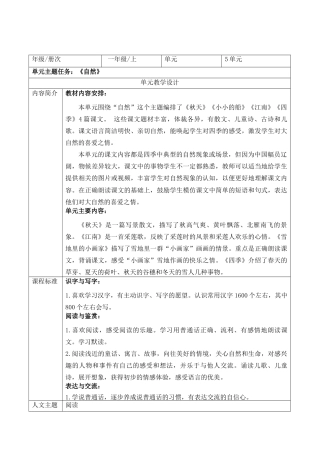 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页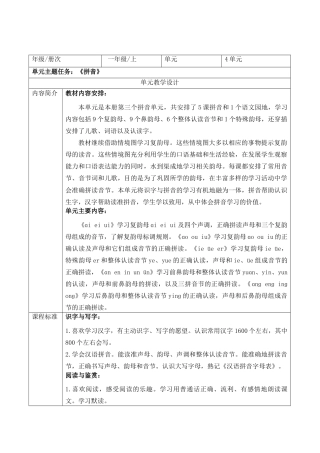 第四单元 整体分析 教学设计.docx24页
第四单元 整体分析 教学设计.docx24页 第二单元 整体分析 教学设计.docx64页
第二单元 整体分析 教学设计.docx64页 13《建筑中的梦想》ppt课件(共18张PPT)-(2025新教材)苏少版八年级上册《美术》4018页
13《建筑中的梦想》ppt课件(共18张PPT)-(2025新教材)苏少版八年级上册《美术》4018页 2024年云南省中考数学试卷(含详细解析).pdf74315页
2024年云南省中考数学试卷(含详细解析).pdf74315页 11.对接达人话术.docx652页
11.对接达人话术.docx652页 党员积分申请表.xlsx1111页
党员积分申请表.xlsx1111页 2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23910页
2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23910页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip4570页
2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip4570页 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页
