微专题常考相似模型模型分析模型一A字型模型展示正A字型斜A字型模型特点有一个公共角∠A模型分析DE∥BC,则∠ADE=∠B,∠AED=∠C∠ADE=∠ACB,∠AED=∠B结论△ADE∽△ABC△ADE∽△ACB模型应用第1题图1.如图,已知∠ACD=∠B,若AC=6,AD=4,BC=10,则CD长为________.2032.如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,ADBC=,若∠AED=∠C,则DE的长为_______.若∠AED=∠B,则DEAC的值为________.252第2题图...
微专题遇到中点如何添加辅助线方法一构造中位线方法解读情形1图形中出现两个及以上的中点时,考虑连接两个中点构造中位线情况一:已知点D、E分别为AB、AC的中点.【结论】DE∥BC,DE=BC,△ADE∽△ABC.12情形2图形中出现中点时,考虑过中点作另一边的平行线构造中位线情况二:已知点D为AB的中点.【结论】AE=CE,DE=BC,△ADE∽△ABC.12针对训练1.如图,在△ABC中,点D,E分别是BC,AC的中点,AD与BE相交于点F.若BF=6,则BE...
微专题遇到角平分线如何添加辅助线方法一过角平分线上一点向角两边作垂线方法解读如图,已知∠MON,点P是∠MON平分线上一点.过角平分线上的点向角两边作垂线.已知PA⊥OM,添加辅助线,作PB⊥ON于点B.结论:PA=PB,OA=OB,∠APO=∠BPO等.1.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AC=4,BC=3,则CD的长为________.第1题图432.如图,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=5,AB=...
微专题等腰、直角三角形的边或角不确定类型一与等腰三角形有关的分类讨论情况一顶角和底角不确定而产生的分类讨论已知等腰三角形的一个角为α(0°<α<90°),确定顶角或底角的度数时,分两种情况:①当α为顶角时,底角为(180°-α);②当α为底角时,顶角为180°-2α.12对于等腰三角形的腰和底不确定的问题,需分三种情况讨论,以等腰△ABC为例:①以BC为底边,AB=AC;②以AC为底边,BA=BC;③以AB为底边,CA=CB.情况二...
微专题常考全等模型模型一平移型模型分析模型展示已知BE=CF,AB∥DE,AC∥DF.模型特点沿同一直线(BC)平移可得两个三角形重合解题思路证明三角形全等的关键:(1)加(减)CE,得BC=EF;(2)利用平行线性质找对应角相等模型应用1.如图,点B,E,C,F在一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.第1题图证明: BE=CF,∴BE+EC=CF+EC,即BC=EF.在△ABC和△DFE中,∴△ABC≌△DFE∴∠A=∠D,ABDFACDEBCFE...
2024江苏中考数学二轮专题复习逆等线之乾坤大挪移题型一平移,对称或构造平行四边形2022年四川省内江中考2022滨州中考题型二构造SAS型全等拼接线段2022贵州遵义统考中考真题2023日照二模2023咸阳二模2023深圳中学联考2023甘肃武威中考真题拆解2023黄冈中考真题拆解题型三构造相似求加权线段和2023年成都市天府新区二模2022广州中考真题(7种解法)2023湖北黄石中考拆解题型四取到最小值时对其它量进行计算湖北武汉中考真题一、...
2024江苏中考数学二轮专题复习逆等线之乾坤大挪移01题型解读题型一平移,对称或构造平行四边形2022年四川省内江中考2022滨州中考题型二构造SAS型全等拼接线段2022贵州遵义统考中考真题2023日照二模2023咸阳二模2023深圳中学联考2023甘肃武威中考真题拆解2023黄冈中考真题拆解题型三构造相似求加权线段和2023年成都市天府新区二模2022广州中考真题(7种解法)2023湖北黄石中考拆解题型四取到最小值时对其它量进行计算湖北武汉中...
2024湖南中考数学二轮专题训练题型一规律探索题类型一数式规律湖南中考真题精选1.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,,试猜想,32016的个位数字是________.2.观察等式:2+22=23-2,2+22+23=24-2,2+22+23+24=25-2,,已知按一定规律排列的一组数:2100,2101,2102,,2199,若2100=m,用含m的代数式表示这组数的和是________.3.观察下面的变化规律:21×3=1-13,23×5=13-15...
2024湖南中考数学二轮专题训练题型一规律探索题类型一数式规律湖南中考真题精选1.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,,试猜想,32016的个位数字是________.2.观察等式:2+22=23-2,2+22+23=24-2,2+22+23+24=25-2,,已知按一定规律排列的一组数:2100,2101,2102,,2199,若2100=m,用含m的代数式表示这组数的和是________.3.观察下面的变化规律:=1-,=-,=-,=-,根...
河南9年真题子母题21考点精讲第四节分式课标要求命题点1分式有意义的条件(2021.11)了解分式和最简分式的概念.考情及趋势分析考情分析年份题号题型分值考查内容202111填空题3分式有意义的条件课标要求命题点2分式的化简及求值(9年8考,仅2017年未考查)1.能用提公因式法、公式法(直接利用公式不超过二次)进行因式分解(指数是正整数);2.能利用分式的基本性质进行约分和通分;3.能进行简单的分式加、减、乘、除运算.考情及趋势分...
河南9年真题子母题21考点精讲第二节实数的运算及大小比较加减乘除实数的大小比较二次根式的估值实数的运算二次根式的性质数轴比较法类别比较法差值比较法平方比较法零次幂乘方特殊角的三角函数值去绝对值符号负整数指数幂常见的开方-1的奇偶次幂二次根式的运算实数的运算及大小比较考点精讲实数的大小比较数轴比较法:数轴上两个点表示的数,右边的点表示的数总比左边的点表示的数类别比较法:正数>0>负数;两个负数比较大小...
四边形多边形特殊四边形的性质与判定多边形正多边形平行四边形矩形菱形正方形性质判定边角对角线对称性定义、性质一题串讲重难点2河南9年真题子母题31考点精讲第一节(特殊)平行四边形的性质(含多边形)课标要求1.了解多边形的定义,多边形的顶点、边、内角、外角、对角线;探索并掌握多边形内角和与外角和公式;2.理解平行四边形、矩形、菱形、正方形、梯形(2022年版课标新增)的概念,以及它们之间的关系;了解四边形的不稳定性...
四边形中的三角形问题第三节考情及趋势分析命题点借助三角形解决特殊四边形问题(9年14考)考情分析年份题号题型分值背景设问涉及三角形的知识点202323(3)解答题2平行四边形求线段长三角形的中位线20225选择题3菱形求菱形的周长中位线202223解答题10矩形、正方形(1)求角度;(2)求角度,判断角度之间的数量关系;(3)求线段长锐角三角函数,全等,勾股定理20219选择题3平行四边形结合平面直角坐标系求点坐标相似,勾股定理考情分析...
遇到中点如何添加辅助线微专题一阶方法训练方法解读情形1当图形中出现两个中点时,考虑构造中位线如图,D,E分别为AB,AC的中点,连接DE.【结论】DE∥BC;DE=BC;△ADE∽△ABC.12方法一构造中位线(9年3考)情形2当图形中出现中点,考虑过中点作已知边的平行线构造中位线如图,点D为AB的中点,过点D作DE∥BC交AC于点E.【结论】AE=CE;DE=BC;△ADE∽△ABC.12例1如图,O为▱ABCD的对角线AC和BD的交点,E为边BC的中点,连接AE交B...
遇到角平分线如何添加辅助线微专题一阶方法训练方法解读情形1利用角平分线的性质“过角平分线上的点向角两边作垂线”构造全等三角形如图,点P是∠MON平分线上的一点.【结论】AP=BP,Rt△AOP≌Rt△BOP.方法一构造对称图形方法解读情形2利用角平分线的性质截取“等线段”构造全等三角形如图,点P是∠MON的平分线上一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPA≌△OPB.可记为“图中有角平分线,可将图形对折...
特殊三角形的分类讨论微专题考情及趋势分析考情分析年份题号题型分值题目背景涉及到的三角形分类讨论类型结合知识点202315填空题3无图,矩形直角三角形直角三角形直角顶点不确定矩形的性质,中位线的性质,勾股定理201815填空题3角为背景作对称直角三角形直角三角形直角顶点不确定中位线的性质,含30°角直角三角形的性质,正方形的判定及性质201715填空题3等腰直角三角形为背景折叠直角三角形直角三角形直角顶点不确定平行线分...
三角形相交线与平行线一般三角形全等与相似三角形基本性质等腰三角形直角三角形等边三角形性质判定面积全等、相似三角形的性质全等、相似三角形的判定特殊三角形线段、直线角、角平分线相交线、平行线命题、定理锐角三角函数锐角三角函数的实际应用解决问题角边角关系边重要线段(角平分线、中线、高线)河南9年真题子母题21考点精讲第一节线段、角、相交线与平行线线段和直线角及其平分线相交线平行线比例线段命题两个基本事实两...
全等、相似三角形的常考模型第五节考情及趋势分析一、一线三等角模型(9年3考)考情分析年份题号题型分值背景结合知识点涉及模型202222解答题10滚铁环切线的性质,平行线的性质或余角、补角或四边形的内角和证明两角之和为90°,利用三角函数求线段长一线三等角型同侧直角相似201915填空题3矩形的折叠相似,勾股定理,解一元二次方程,解一元一次方程,正方形的判定与性质,折叠的性质一线三等角型同侧直角相似201615填空题3图形...
一题串讲重难点21考点精讲第三节特殊三角形及其性质课标要求1.了解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两底角相等;底边上的高线、中线及顶角平分线重合.探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形.探索等边三角形的性质定理:等边三角形的各角都等于60°,及等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形;(2022年版课标将“...
一题串讲重难点2河南9年真题子母题31考点精讲课时2锐角三角函数与相似三角形的实际应用课标要求考情及趋势分析命题点1相似三角形的实际应用(2023年新考查)会利用图形的相似解决一些简单的实际问题.考情分析年份题号题型分值考查内容结合知识点202320解答题9用自制的测高仪测树高相似课标要求1.探索并认识锐角三角函数(sinA,cosA,tanA),知道30°,45°,60°角的三角函数值;2.会使用计算器由已知锐角求它的三角函数值,由已...
 2024年云南省中考数学试卷(含详细解析).pdf74315页
2024年云南省中考数学试卷(含详细解析).pdf74315页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip457
2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip457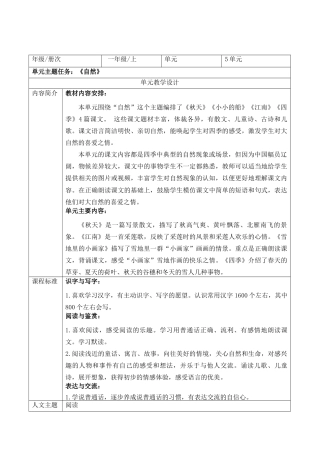 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页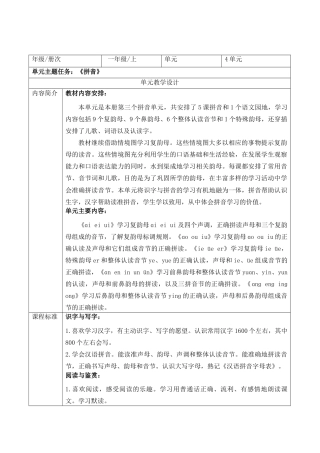 第四单元 整体分析 教学设计.docx24页
第四单元 整体分析 教学设计.docx24页 第二单元 整体分析 教学设计.docx64页
第二单元 整体分析 教学设计.docx64页 13《建筑中的梦想》ppt课件(共18张PPT)-(2025新教材)苏少版八年级上册《美术》4018页
13《建筑中的梦想》ppt课件(共18张PPT)-(2025新教材)苏少版八年级上册《美术》4018页 2024年云南省中考数学试卷(含详细解析).pdf74315页
2024年云南省中考数学试卷(含详细解析).pdf74315页 11.对接达人话术.docx652页
11.对接达人话术.docx652页 党员积分申请表.xlsx1111页
党员积分申请表.xlsx1111页 2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23910页
2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23910页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip4570页
2025届高三第一次八省联考(T8联考)英语 (精校版)(试题+详解+音频).zip4570页 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页
