2024海南中考数学二轮专题训练几何图形折叠型综合题(小题破大题)方法再现:沿图形上一顶点所在的直线折叠1.如图,折叠矩形纸片ABCD,先折出折痕BD,展开后再折叠,使AD落在对角线BD上,点A的对应点是A′,得折痕DG.若AB=2,BC=1,求AG的长.【思维教练】根据折叠的性质求出折叠后对应边的长,再利用勾股定理求解即可.第1题图方法再现:沿特殊四边形的对角线折叠2.如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E,...
2024海南中考数学二轮专题训练几何图形折叠型综合题(小题破大题)方法再现:沿图形上一顶点所在的直线折叠1.如图,折叠矩形纸片ABCD,先折出折痕BD,展开后再折叠,使AD落在对角线BD上,点A的对应点是A′,得折痕DG.若AB=2,BC=1,求AG的长.【思维教练】根据折叠的性质求出折叠后对应边的长,再利用勾股定理求解即可.第1题图方法再现:沿特殊四边形的对角线折叠2.如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E,...
2024海南中考数学二轮专题训练几何图形旋转型综合题(小题破大题)模型再现:轴对称(翻折)型全等模型1.如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM,求证:EF=CF+AE.【思维教练】由旋转可得DE=DM,∠EDM=90°,由∠EDF=45°,得到∠MDF=45°,即∠EDF=∠MDF,再由DF=DF,可证△DEF≌△DMF,由全等三角形的对应边相等可得出EF=CF+AE.第1题图模型再现:...
2024海南中考数学二轮专题训练几何图形旋转型综合题(小题破大题)模型再现:轴对称(翻折)型全等模型1.如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM,求证:EF=CF+AE.【思维教练】由旋转可得DE=DM,∠EDM=90°,由∠EDF=45°,得到∠MDF=45°,即∠EDF=∠MDF,再由DF=DF,可证△DEF≌△DMF,由全等三角形的对应边相等可得出EF=CF+AE.第1题图模型再现:...
2024海南中考数学二轮专题训练几何图形非动态型综合题(小题破大题)模型再现:自旋转型全等模型1.如图,点E在正方形ABCD的边CD上,点F为CB延长线上一点,且DE=BF,连接AE,AF.求证:AE=AF.【思维教练】要证AE=AF,只需证△ADE≌△ABF第1题图模型再现:8字型相似模型2.如图,在正方形ABCD中,AC为对角线,点F为CD上一点,连接BF交AC于点E.求证:△ABE∽△CFE.【思维教练】要证△ABE∽△CFE,需在△ABE和△CFE中找出对应角相等...
2024海南中考数学二轮专题训练几何图形非动态型综合题(小题破大题)模型再现:自旋转型全等模型1.如图,点E在正方形ABCD的边CD上,点F为CB延长线上一点,且DE=BF,连接AE,AF.求证:AE=AF.【思维教练】要证AE=AF,只需证△ADE≌△ABF第1题图模型再现:8字型相似模型2.如图,在正方形ABCD中,AC为对角线,点F为CD上一点,连接BF交AC于点E.求证:△ABE∽△CFE.【思维教练】要证△ABE∽△CFE,需在△ABE和△CFE中找出对应角相等...
2024海南中考数学二轮专题训练几何图形动点型综合题(小题破大题)模型再现:自旋转型全等模型1.如图,在矩形ABCD中,点E是BC上一动点,连接DE,点F是DE上一点,DF=CE,BC=DE.求证:AF⊥DE.【思维教练】由矩形ABCD的性质可知∠ADF=∠DEC,由BC=DE,得AD=DE,再由已知条件DF=CE,即可证得△ADF≌△DEC,可得∠AFD=∠C=90°,即可得证.第1题图模型再现:一线三垂直型相似模型2.如图,在矩形ABCD中,AB=4,BC=5,E是BC边...
2024海南中考数学二轮专题训练几何图形动点型综合题(小题破大题)模型再现:自旋转型全等模型1.如图,在矩形ABCD中,点E是BC上一动点,连接DE,点F是DE上一点,DF=CE,BC=DE.求证:AF⊥DE.【思维教练】由矩形ABCD的性质可知∠ADF=∠DEC,由BC=DE,得AD=DE,再由已知条件DF=CE,即可证得△ADF≌△DEC,可得∠AFD=∠C=90°,即可得证.第1题图模型再现:一线三垂直型相似模型2.如图,在矩形ABCD中,AB=4,BC=5,E是BC边...
微专题遇到中点如何添加辅助线方法一构造中位线情形1图形中出现两个及以上的中点时,考虑连接两个中点构造中位线如图,已知点D、E分别为AB、AC的中点.【结论】DE∥BC,DE=12BC,△ADE∽△ABC.情形2图形中出现中点时,考虑过中点作另一边的平行线构造中位线如图,已知点D为AB的中点.【结论】AE=CE,DE=12BC,△ADE∽△ABC.1.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=6,则BF的长为()A...
微专题遇到角平分线如何添加辅助线方法一过角平分线上一点向角两边作垂线如图,点P是∠MON的平分线上一点,PA⊥OM于点A.【结论】PB=PA,△AOP≌△BOP.1.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AC=4,BC=3,则CD的长为.第1题图432.如图,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=5,AB=20,则△AOB的面积是.第2题图503.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E,∠B=30...
微专题四大常考相似模型模型一A字型模型展示1.正A字型:当有一组对应边平行(DE∥BC)时,根据同位角相等可得到另外一组对应角相等,得这两个三角形相似,为正A字型线簇型:DE∥BC模型展示2.斜A字型:当对应边都不平行(DE与BC不平行)时,根据条件找另外一组对角相等或者公共角的两边对应成比例,得到这两个三角形相似,为斜A字型(双垂直共角夹线型)模型特点两个三角形有一个公共角∠BAC结论1.通用结论:△ADE∽△ABC或△ADE∽△...
微专题七大常考全等模型模型一平移型模型展示模型特点沿同一直线(BC)平移可得两三角形重合(BE=CF)解题思路证明三角形全等的关键:(1)加(减)共线部分CE,得BC=EF;(2)利用平行线性质找对应角相等1.如图,点C是AE的中点,∠A=∠ECD,AB=CD,若∠B=50°,则∠D的度数为()A.30°B.40°C.50°D.60°第1题图C2.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.第2题图证明: BE=CF,∴BE+EC=C...
微专题跨学科试题【全国视野解读】《教育部关于加强初中学业水平考试命题工作的意见》中指出“积极探索跨学科命题”.该命题模式让学生体会数学与其他学科之间的联系.通过学科知识间的融合,提升学生运用所学知识解决复杂问题的能力,故推荐此题型高效备考.目前各地中考命题都在陆续融入跨学科试题.1.[跨生物学科]——遗传基因根据生物学家的研究,人体的许多特征都是由基因控制的.有的人是单眼皮,有的人是双眼皮,这是由...
微专题二次函数与相似三角形问题例如图①,抛物线y=ax2+2x+c与x轴交于点A,B(6,0),与y轴交于点C(0,6),连接AC,BC.(1)求抛物线的解析式;例题图①【思维教练】将B,C两点坐标代入抛物线解析式中即可求解.解:将B(6,0),C(0,6)代入y=ax2+2x+c,得36a+12+c=0c=6,解得a=-12c=6,∴抛物线的解析式为y=-12x2+2x+6;例题图①(2)如图②,点N是y轴上的点,连接AN,若△AON∽△CAN(不包含全等),求点N的坐标;例...
微专题二次函数与线段、周长问题例如图①,已知抛物线的顶点坐标为M(1,278),且抛物线与x轴交于A(-2,0),B(4,0)两点,与y轴交于点C,对称轴为直线l,直线y=kx+b与抛物线交于B,C两点.例题图①(1)求抛物线的解析式;解: 抛物线与x轴的交点为A(-2,0),B(4,0),∴可设抛物线的解析式为y=a(x+2)(x-4)(a≠0), 抛物线的顶点坐标为M(1,278),将点M的坐标代入抛物线解析式得,a=-38,∴抛物线的解析式为y=-38x2+...
微专题二次函数与特殊四边形问题例如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(5,0)两点,与y轴交于点C,连接BC.(1)求抛物线的解析式;解:将A(1,0),B(5,0)代入y=-x2+bx+c中,得-1+b+c=0-25+5b+c=0,解得b=6c=-5,∴抛物线的解析式为y=-x2+6x-5;【思维教练】将点A,C的坐标代入抛物线解析式中即可求解.例题图①(2)如图②,若点D是平面内一点,是否存在点D,使得以AB为边,且以A,B,C,D为顶点的...
微专题二次函数与特殊三角形问题例如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3),抛物线顶点为D,对称轴DF交BC于点E,交x轴于点F.(1)求抛物线的解析式;例题图①【思维教练】已知抛物线与x轴的交点,可设抛物线的解析式为交点式y=a(x+1)(x-3),代入点C坐标即可求解.解: 抛物线与x轴交于A(-1,0),B(3,0)两点,∴可设抛物线解析式为y=a(x+1)(x-3),将点C(0,3)代入,得a=-1,∴抛物线解析...
微专题二次函数与面积问题例抛物线y=-x2-2x+3与x轴交于A,B两点,与y轴交于点C,直线y=x+3与抛物线交于A,C两点.(1)如图①,若点P为抛物线上一点,且点P的横坐标为-2,连接PA,PC,求△PAC的面积;例题图①【思维教练】由抛物线解析式可以得出点C的坐标,根据点P的横坐标为2及三角形的面积公式即可求解.解: 抛物线的表达式为y=-x2-2x+3,令x=0,得y=3,∴C(0,3)∴抛物线的对称轴为直线x=-1, 点P的横坐标...
微专题二次函数与角度问题例如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于点C,其中A(-6,0),B(2,0),C(0,-3).(1)求抛物线解析式;例题图①【思维教练】利用待定系数法求解析式即可.解:将点A、B、C的坐标代入抛物线解析式得,36a-6b+c=04a+2b+c=0c=-3,解得a=14b=1c=-3,∴抛物线的解析式为y=14x2+x-3;例题图①(2)如图②,在抛物线上是否存在一点P(不与点A,B重...
微专题对称性质在折叠问题中的应用1.折叠问题常见的类型有:2.折叠问题的本质是全等变换,折叠前的部分与折叠后的部分是全等图形.①线段相等:ED′=______,EG=______,FD′=______;②角度相等:∠D′=________,∠D′EG=________;③全等关系:四边形FD′EG≌_____________.ADAGFD∠D∠DAG四边形FDAG3.折痕可看作垂直平分线:GF⊥________(折痕垂直平分连接两个对应点的连线).4.折痕可看作角平分线:∠EGF=______...
 GB 55031-2022 民用建筑通用规范.pdf(24页)182124页
GB 55031-2022 民用建筑通用规范.pdf(24页)182124页 2024年云南省中考数学试卷(含详细解析).pdf74315页
2024年云南省中考数学试卷(含详细解析).pdf74315页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 苏州科技学院-826物理化学【2012】考研真题364页
苏州科技学院-826物理化学【2012】考研真题364页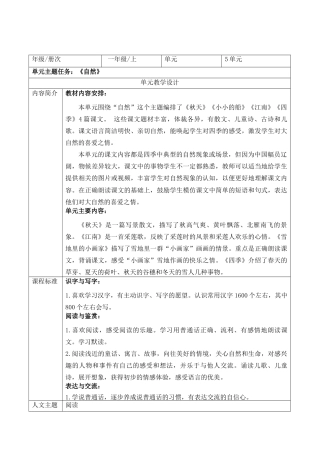 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页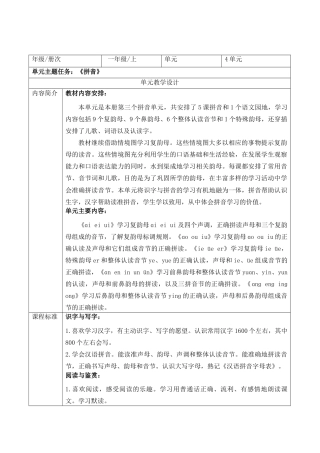 第四单元 整体分析 教学设计.docx24页
第四单元 整体分析 教学设计.docx24页 第二单元 整体分析 教学设计.docx64页
第二单元 整体分析 教学设计.docx64页 GB 55031-2022 民用建筑通用规范.pdf(24页)182124页
GB 55031-2022 民用建筑通用规范.pdf(24页)182124页 2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23910页
2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23910页 党员积分申请表.xlsx1111页
党员积分申请表.xlsx1111页 11.对接达人话术.docx652页
11.对接达人话术.docx652页 2024年云南省中考数学试卷(含详细解析).pdf74315页
2024年云南省中考数学试卷(含详细解析).pdf74315页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 013130825-方亚楠-三安光电股份有限公司应收账款管理的研究932页
013130825-方亚楠-三安光电股份有限公司应收账款管理的研究932页
