专题五二次函数综合题专题五二次函数综合题类型一线段问题(2023.25)二阶综合训练1.(2023锦江区二诊节选)如图,已知一次函数y=-x+3的图象与y轴,x轴相交于点A,B,抛物线y=-x2+bx+c的顶点M在直线AB上,设点M横坐标为m.(1)如图①,当m=3时,求此时抛物线y=-x2+bx+c的函数表达式;第1题图解:(1)在y=-x+3中,令x=3,得y=0,∴M(3,0),专题五二次函数综合题第1题图∴抛物线y=-x2+bx+c的顶点M的坐标为(3,0),...
第一轮专题复习之专题四几何动态探究题专题四几何动态探究题考情及趋势分析成都8年高频点考情及趋势分析考情分析类型年份题号题型分值考查设问背景图形动点探究题202223B卷填空题4求线段差最大值菱形2020254求线段最值,双空矩形折叠探究题2023224求tanA直角三角形2021244求线段长,双空矩形2018244求线段比值菱形2017254求线段长正方形2016254求线段长的最小值平行四边形平移、旋转探究题2019244求线段和的最小值菱形,三角形...
专题三反比例函数综合题考情及趋势分析成都8年高频点考情及趋势分析考情分析年份题号题型分值考查内容考查设问202024B卷填空题4直线与双曲线结合求点坐标(2个解)2018254结合新定义,直线与双曲线结合求k值2017244结合新定义,直线与双曲线结合求k值【考情总结】考查频次及特点:8年3考,反比函数综合题均在B卷填空题考查,题位在压轴题或者次压轴题,本题的难点不在于计算量,而在于学生的读图能力和理解能力,重点考查学生的思...
专题六综合与实践专题六综合与实践考情及趋势分析成都8年高频点考情及趋势分析考情分析类型年份题号题型分值背景图形考查设问动点问题202326解答题12等腰直角三角形(1)(2)证明线段数量关系;(3)求动点的运动路径长20222612两矩形相似(1)探究三角形相似;(2)(3)求三角函数值20192710等腰三角形(1)证三角形相似;(2)求线段长;(3)探究线段相等,求线段长折叠问题20202710矩形(1)求角度;(2)求线段长;(3)求线段比值专题六综合与实...
专题六综合与实践专题六综合与实践类型三旋转问题(8年3考:2021.27,2018.27,2016.27)满分技法见第一部分微专题图形的旋转1.(2023武侯区模拟)如图,在矩形ABCD中,AB=kBC(0<k<1),将线段AB绕点A逆时针旋转α度(0<α<90)得到线段AE,过点E作AE的垂线交射线CD于点H,交射线AD于点M.第1题图备用图专题六综合与实践【尝试初探】(1)当点M在AD延长线上运动时,∠BAE与∠AME始终相等,且△AEM与△HDM始终相似,请说明理由;第1题...
专题六综合与实践专题六综合与实践类型二折叠问题(2020.27)二阶综合训练1.(2023成都黑白卷)综合与实践问题情境:在数学活动课上,老师给出了这样一个问题:如图①,在正方形纸片ABCD中,点E是边AB的中点,将△BCE沿CE所在的直线折叠,得到△B′CE,延长CB′交AD于点P,连接AB′.猜想证明:(1)求证:∠PAB′=∠PB′A;第1题图专题六综合与实践(1)证明: 四边形ABCD为正方形,∴∠B=∠BAD=90°.由折叠的性质知,△B′CE≌△BC...
2024成都中考数学第一轮专题复习之重点、难点知识强化训练第1天打卡:____月____日1.[新考法—过程性学习]在数学活动课上,老师展示了如下问题,请同学们进行思考求解.已知点A,B,C在数轴上表示的数分别为,3(x-1),9-x,且点A在点B的左侧,点C在点B的右侧,求x的取值范围.小云的分析过程如下:第一步:根据点A在点B的左侧,可列不等式为______________①;第二步:根据点C在点B的右侧,可列不等式为________________②;...
2024成都中考数学第一轮专题复习之第四章微专题一线三等角模型解决全等、相似问题知识精练1.如图,△ABC为等边三角形,D是BC上一点,连接AD,点P,Q在AD上,连接BP,CQ,且∠BPD=∠CQD=60°,若BP=3,CQ=5,则PQ的长为________.第1题图2.如图,在四边形ABCD中,AD=4,AB=10,点E是AB的中点,连接DE,CE,若∠A=∠B=∠DEC,则BEBC的值为________.第2题图3.(2023重庆A卷)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为...
微专题与线段最值有关的问题微专题与线段最值有关的问题考情及趋势分析成都8年高频点考情及趋势分析考情分析类型年份题号题型分值考查内容结合知识点一条线段求最值202127解答题10利用“三角形三边关系”求最小值全等三角形,三角形的中位线20182710利用“垂线段最短”求最小值三角形面积201625B卷填空题4利用“垂线段最短”求最小值图形的折叠,全等三角形,平行四边形的性质微专题与线段最值有关的问题考情分析类型年份题号题...
微专题辅助圆微专题辅助圆一阶方法突破方法解读如图,在平面内,点A为定点,点B为动点,且AB长度固定,则动点B的轨迹是以点A为圆心,AB长为半径的圆或圆弧.推广:在折叠或旋转问题中,有时会利用“定点定长作圆”模型确定动点的运动轨迹.方法一定点定长作圆微专题辅助圆例1如图,在矩形ABCD中,BC=4,AB>2,若CE=2,且点E在矩形ABCD的内部,则∠ABE的度数可能是()A.30°B.40°C.60°D.90°例1题图C解题关键点求∠ABE可能的...
2024成都中考数学第一轮专题复习之第四章第三节全等与相似三角形的性质与判定(含位似)知识精练基础题1.(2023长春)如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA′、BB′的中点,只要量出A′B′的长度,就可以知道该零件内径AB的长度.依据的数学基本事实是()第1题图A.两边及其夹角分别相等的两个三角形全等B.两角及其夹边分别相等的两个三角形全等C.两条直线被一组平行线所截,所得的对应线段成比例D.两点之间...
2024成都中考数学第一轮专题复习之第三章第四节函数与方程(组)不等式(组)的关系知识精练基础题1.已知一次函数y=kx+b(k≠0)的图象过A(2,0),B(0,4)两点.则关于x的方程kx+b=0的解是()A.x=1B.x=2C.x=3D.x=42.(2023宁波)如图,一次函数y1=k1x+b(k1>0)的图象与反比例函数y2=k2x(k2>0)的图象相交于A,B两点,点A的横坐标为1,点B的横坐标为-2,当y1<y2时,x的取值范围是()A.x<-2或x>1B.x<-2或0<x<1C.-2<x<0或x>1D....
2024成都中考数学第一轮专题复习之第三章微专题二次函数图象与系数a,b,c的关系1.(2023贵州)已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,b)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限第1题图2.如图,二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B两点,对称轴是直线x=1,下列说法正确的是()第2题图A.a>0B.b>0C.点B的坐标为(4,0)D.当x>-1时,y的值随x值的增大而增大3.(2023日照)在平面直角坐标...
第一章第一节实数(含二次根式)第一节实数(含二次根式)基础题1.(2023江西)下列各数中,正整数是()A.3B.2.1C.0D.-22.(2023武汉)实数3的相反数是()A.3B.C.-D.-33.(2023烟台)-的倒数是()A.B.C.-D.-13132323233232ADD第一节实数(含二次根式)4.(2023大连)-6的绝对值是()A.-6B.6C.D.-16165.(2023舟山)-8的立方根是()A.-2B.2C.±2D.不存在6.(2023河南)下列各数中最小的数是()A.-1B.0C.1D.3BAA第一节实数(含二次根式...
成都8年真题子母题21考点精讲第一章第一节实数(含二次根式)考点精讲实数的分类按定义分有理数整数分数有限小数或无限循环小数无理数:________________无理数的常见形式:1.开方开不尽的数,如,,等2.含有根号的三角函数值,如tan30°,sin45°等3.π及化简后含有π的数,如,等(负面清单)4.有规律的无限不循环小数,如0.101001(相邻两个1之间依次多一个0)按大小分:正数、0、负数,其中0既不是正数也不是负数.注:常用...
第三节分式及其运算第三节分式及其运算基础题1.(2022怀化)代数式x,,,x2-,,中,属于分式的有()A.2个B.3个C.4个D.5个2.下列分式中是最简分式的是()251224x231x12xx21xx42x211xx11xxBA第三节分式及其运算3.(北师八下P110习题第2题改编)若分式有意义,则实数x的取值范围是()A.x≠B.x≠-C.x>D.x<23xx322332234.(2023河南)化简的结果是()A.0B.1C.aD.a-25.(2023凉山州)若分式的值为0,则x的值是()A.0B.-1...
成都8年真题子母题21考点精讲第三节分式及其运算课标要求成都8年高频点考情及趋势分析命题点分式化简及求值(8年8考)1.了解分式和最简分式的概念;2.能利用分式的基本性质进行约分和通分;3.能进行简单的分式加、减、乘、除运算.考情及趋势分析考情分析类型年份题号题型分值考查形式所代值化简结果分式化简求值202319B卷填空题4(1-A)÷B3ab-3b2-2=0ab-b2202219B卷填空题4(A-B)÷C,A为整式2a2-7=2aa(a-1)202116解答题6...
第一章第二节代数式、整式及因式分解第二节代数式、整式及因式分解基础题1.(北师七上P83内文改编)如图是一个数值转换机,若输入a的值为-3,则输出的结果为()A.4B.-4C.5D.-5第1题图A第二节代数式、整式及因式分解2.(2023扬州)若()2a2b=2a3b,则括号内应填的单项式是()A.aB.2aC.abD.2ab3.(2023江西)计算(2m2)3的结果为()A.8m6B.6m6C.2m6D.2m54.下列计算正确的是()A.(a+b)2=a2+b2B.(-ab)2a=-a2b2C.5a4b÷ab=5a3D.a22a2...
第二节代数式、整式及因式分解成都8年真题子母题21考点精讲课标要求成都8年高频点考情及趋势分析命题点1整式的运算(8年9考)1.了解整数指数幂的意义和基本性质;2.理解整式的概念,掌握合并同类项和去括号的法则;3.能进行简单的整式加法和减法运算;能进行简单的整式乘法运算(其中多项式相乘仅指一次式之间以及一次式与二次式相乘);4.能推导乘法公式:(a+b)(a-b)=a2-b2,(a±b)2=a2±2ab+b2,了解公式的几何背景,并能利...
微专题对角互补模型微专题对角互补模型1.问题呈现:已知等边△ABC边BC的中点为D,∠EDF=120°,且点E,F分别在AB,AC上,现要探究线段BE,CF与BC之间的数量关系.【特例研究】(1)如图①,当DE⊥AB,DF⊥AC时,请直接写出BE,CF与BC之间的数量关系:_______________;第1题图①BE+CF=BC12微专题对角互补模型【类比探究】(2)如图②,当∠DEB≠∠DFC时,(1)中的结论是否仍然成立?若成立,请给出证明过程,若不成立,请说明理由...
 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 11.对接达人话术.docx642页
11.对接达人话术.docx642页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23810页
2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23810页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 25年WP过AI率汉语言文学-论《左传》中季孙氏家族的叙事特色10.410.docx1825页
25年WP过AI率汉语言文学-论《左传》中季孙氏家族的叙事特色10.410.docx1825页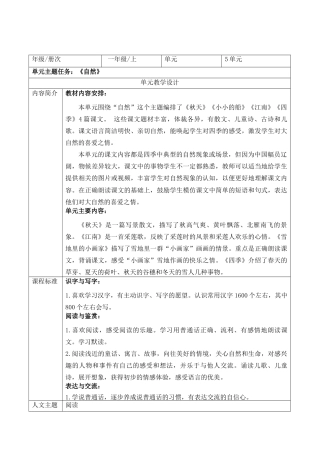 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页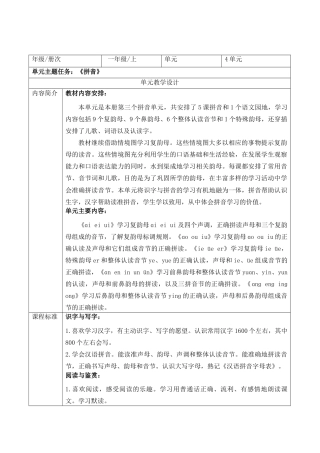 第四单元 整体分析 教学设计.docx24页
第四单元 整体分析 教学设计.docx24页 第二单元 整体分析 教学设计.docx64页
第二单元 整体分析 教学设计.docx64页 第一单元 整体分析 教学设计.docx165页
第一单元 整体分析 教学设计.docx165页 11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页
11《刀言纸语》ppt课件(共27张PPT)-(2025新教材)苏少版八年级上册《美术》927页 11.对接达人话术.docx642页
11.对接达人话术.docx642页 19DX101-1建筑电气常用数据(带书签).pdf3399354页
19DX101-1建筑电气常用数据(带书签).pdf3399354页 2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23810页
2024年1月浙江省普通高校招生选考科目考试历史试题 (含答案).docx23810页 (学习资料)小六壬预测法中251页
(学习资料)小六壬预测法中251页 25年WP过AI率汉语言文学-论《左传》中季孙氏家族的叙事特色10.410.docx1825页
25年WP过AI率汉语言文学-论《左传》中季孙氏家族的叙事特色10.410.docx1825页 第五单元 整体分析 教学设计.docx74页
第五单元 整体分析 教学设计.docx74页 第四单元 整体分析 教学设计.docx24页
第四单元 整体分析 教学设计.docx24页 第二单元 整体分析 教学设计.docx64页
第二单元 整体分析 教学设计.docx64页
